引言

👆这些话听起来熟悉吗?如果你也说过类似的话,那么恭喜你,你已经掉进了人类大脑最常见的认知陷阱之一。
事实是:
- 飞机是最安全的交通工具,事故率远低于汽车
- 彩票中头奖的概率比被雷劈还低
- 被鲨鱼咬的概率远低于被自动售货机砸死
🤔 但为什么我们的感觉和事实完全相反?
今天,我们来聊聊两个有趣的认知偏差——几率谬误(Probability Fallacy)和几率忽视(Probability Neglect)。它们解释了为什么我们总是在概率判断上犯错,以及如何做出更理性的决策。
什么是几率谬误和几率忽视
几率谬误(Probability Fallacy)
几率谬误是指人们倾向于高估小概率事件发生的可能性,或者低估大概率事件发生的可能性。
典型表现:
- 害怕坐飞机,觉得会坠机(实际概率:千万分之一)
- 相信自己能中彩票(实际概率:千万分之一)
- 担心被恐怖袭击(实际概率:百万分之一)
简单来说,就是把小概率当大概率,把大概率当小概率。
几率忽视(Probability Neglect)
几率忽视是指人们在面对强烈情绪时,完全忽略实际概率,只关注结果的严重性。
典型表现:
- 看到飞机失事新闻后,不管概率多低都不敢坐飞机
- 听说疫苗有副作用,不管概率多小都拒绝接种
- 担心核电站泄漏,不管安全措施多完善都反对建设
- 害怕被绑架,不管实际风险多低都不让孩子独自出门
简单来说,就是根本不看概率,只看后果有多可怕。
两者的关系
这两个偏差经常一起出现:
| 认知偏差 | 核心问题 | 典型场景 |
|---|---|---|
| 几率谬误 | 错误估计概率大小 | "我觉得会中彩票" |
| 几率忽视 | 完全不考虑概率 | "不管概率多低,我都不坐飞机" |
几率谬误是算错了,几率忽视是不算了。
为什么我们会犯这些错误:四大心理机制
其实,这不是智商问题,也不是数学问题,而是人类大脑的工作机制。
1. 可得性启发(Availability Heuristic)
核心原理:我们的大脑有个特点——越容易想起的事情,就觉得越常见。
心理学家阿莫斯·特沃斯基(Amos Tversky)和丹尼尔·卡尼曼(Daniel Kahneman)在1973年提出了这个概念,并因此获得了诺贝尔经济学奖。
为什么会这样?
1)因为大脑在判断概率时,不是去查统计数据,而是问自己:"我能想起多少个这样的例子?"
2)媒体报道给人造成偏差的:
- 飞机失事会上头条,连续报道好几天;每天安全降落的几万架次航班不会被报道
- 彩票中奖者会成为新闻人物;几亿没中奖的人不会被提及
- 鲨鱼袭击会成为热点;每年被蜜蜂蜇死的人(更多)不会被关注
因为媒体报道的偏差,我们的感知完全扭曲了。
2. 情绪压倒理性(Affect Heuristic)
核心原理:当情绪强烈时,大脑的理性思考区域会被抑制。
神经科学研究发现,当人们感到恐惧、愤怒或兴奋时:
- 杏仁核(情绪中枢)高度活跃
- 前额叶皮层(理性思考区)活动减弱
- 决策完全由情绪主导
典型场景:
看到飞机坠毁的画面时,你感受到的是:
- 恐惧:失控、坠落、死亡
- 画面:火光、残骸、哭泣的家属
- 想象:如果是我怎么办
这种强烈的情绪会让你完全忽略"概率只有千万分之一"这个事实。
3. 损失厌恶(Loss Aversion)
核心原理:人类对损失的敏感度,是对收益的2-3倍。这是卡尼曼和特沃斯基提出的另一个重要概念。
简单来说:失去100块的痛苦 > 得到100块的快乐;
在概率判断中的表现:我们对负面小概率事件的关注,远超过正面大概率事件:
- 飞机失事的恐惧(小概率) > 安全到达的安心(大概率)
- 投资亏损的痛苦(中概率) > 投资盈利的喜悦(中概率)
进化解释:在远古时代,这是生存优势:错过一次捕猎机会:饿一顿(不致命);忽视一次危险信号:被吃掉(致命)
这在远古时代是优势,但在现代社会,却让我们过度关注小概率的坏事,而忽视大概率的好事。
损失厌恶让投资者陷入'赚小钱、亏大钱'的怪圈:股票涨10%时急于止盈(担心回调),错过后续50%的涨幅;而股票跌10%甚至50%时却拒绝止损(幻想反弹),最终深度套牢。统计显示,突破上涨的股票有60-70%概率继续上涨,而持续下跌的股票也有类似概率继续走低——这就是趋势的力量。
4. 缺乏统计直觉(Innumeracy)
核心原理:人类大脑不是为了处理概率而进化的。
进化视角:在远古时代,看到草丛动了一下,你有两个选择:
选择A:计算概率
- "草丛动了,可能是风(90%),也可能是老虎(10%)"
- "让我算算贝叶斯概率..."
- (被老虎吃掉)
选择B:立刻逃跑
- "管他是什么,先跑再说!"
- (浪费点体力,但活下来了)
那些选择A计算概率的祖先,都被吃掉了。 那些选择B立刻逃跑的祖先,活了下来,成为了我们。
结果:我们继承了"宁可信其有"的基因,倾向于:
- 高估危险的概率
- 快速反应,而非精确计算
- 依赖直觉,而非统计
现代困境:这种机制在远古时代是生存优势,但在现代社会:
- 草丛里没有老虎了
- 但我们还在用同样的大脑
- 结果就是各种概率判断错误
生活中的几率谬误和几率忽视
这两个偏差在生活中无处不在,影响着我们的每一个决策。让我们看看具体的场景。
场景一:彩票与保险的矛盾
有趣的现象:同一个人,可能既买彩票,又买保险。
这很矛盾:买彩票:高估中奖概率(几率谬误);买保险:高估意外概率(几率谬误)
真实概率对比:彩票中头奖概率是 1700 万分之 1,相当于每周买一次,要买32万年;被雷劈死的概率是280万分之一。也就是中彩票比被雷劈死的概率还低。
实际情况:很多人每周买彩票;但不买家财险、意外险
为什么?
- 彩票:正面情绪(兴奋、希望),媒体报道中奖者
- 保险:负面情绪(焦虑、恐惧),但不如彩票有吸引力
- 损失厌恶:买保险感觉是"损失"(交钱),买彩票感觉是"投资"(可能赚钱)
理性的做法:少买彩票(概率太低);多买保险(概率相对高,后果严重)
场景二:投资理财的幻觉
典型想法:"我要买这只股票,肯定能翻倍!"
真实数据:
| 投资者类型 | 长期盈利概率 | 跑赢指数概率 |
|---|---|---|
| 散户 | <10% | <5% |
| 专业投资者 | 30-40% | 15-20% |
| 顶级基金经理 | 50-60% | 20-30% |
| 指数基金 | 100%(跟随市场) | 50%(定义) |
为什么散户还是要炒股?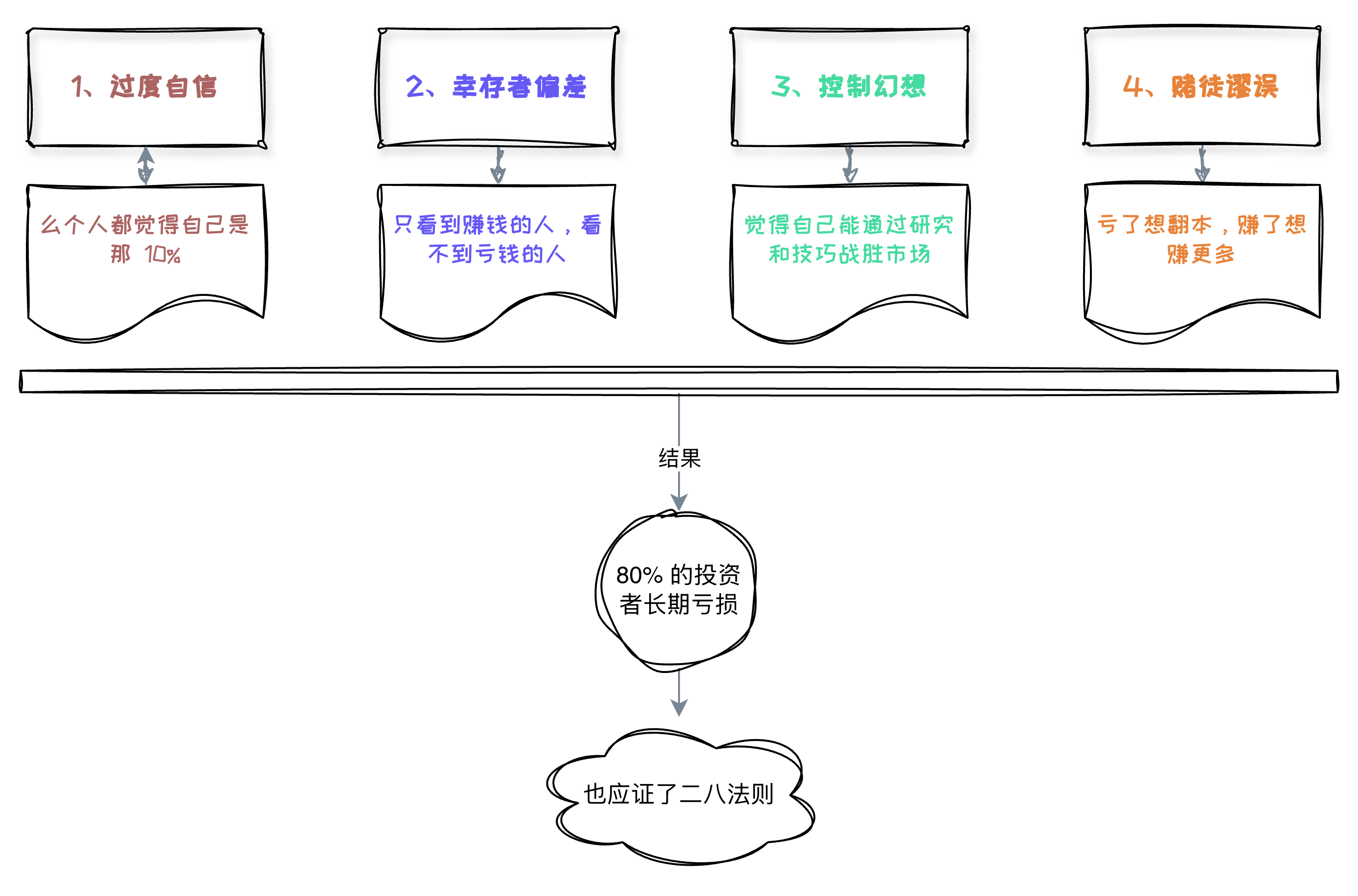
巴菲特的建议:"对于绝大多数投资者来说,最好的选择是买低成本的指数基金。"
场景三:安全焦虑的时代
典型想法:"现在社会太危险了,到处都是坏人!"
真实情况:暴力犯罪率比30年前降低50%;谋杀率处于历史低位;谋杀率年概率<1/100万;整体安全水平是人类历史上最安全的时代。
为什么感觉相反?
- 媒体偏差:坏消息是新闻,好消息不是,"今天没有发生谋杀案"不会上头条","今天发生了一起谋杀案"会连续报道。
- 社交媒体放大:一个坏消息会被转发无数次,每个人都在分享恐惧,形成"恐惧回音室"
- 怀旧偏差:人们总觉得"过去更好",但实际上过去犯罪率更高,只是当时没有24小时新闻和社交媒体
结果:你生活在人类历史上最安全的时代,却感到最不安全。
如何克服这些偏差:六个实用方法
了解了问题,我们该如何克服呢?以下是六个经过验证的方法。
方法一:用数据说话,而非感觉
核心原则:每次做决策前,问自己:"实际概率是多少?"
实践步骤:
- 不要凭感觉,去查实际数据
- 寻找可靠来源:官方统计、科学研究、权威机构
- 避免个案和故事:一个人的经历不代表统计规律
方法二:对比基准线,而非孤立判断
核心原则:不要孤立地看一个风险,要和其他风险对比。
实践方法:列出所有相关风险,进行对比:
例子:核电站安全性
| 能源类型 | 每太瓦时死亡人数 | 相对风险 |
|---|---|---|
| 煤电 | 24.6 | 411倍 |
| 石油 | 18.4 | 307倍 |
| 天然气 | 2.8 | 47倍 |
| 生物质能 | 4.6 | 77倍 |
| 水电 | 1.4 | 23倍 |
| 太阳能 | 0.44 | 7倍 |
| 风能 | 0.15 | 2.5倍 |
| 核能 | 0.06 | 1倍(最安全) |
结论:核电其实是最安全的能源之一,但因为事故太震撼(切尔诺贝利、福岛),人们就高估了风险。
应用到决策:
担心某个风险时,问自己:"和其他选择相比,这个风险大还是小?";"如果避免这个风险,会面临什么其他风险?";"哪个风险更大?"
方法三:警惕情绪绑架,保持冷静
核心原则:当你感到强烈情绪时,暂停决策。
情绪识别清单:当你有以下感受时,要警惕:
- 😱 恐惧:"太可怕了!这绝对不能做!"
- 😡 愤怒:"太过分了!我要报复/反击!"
- 🤩 兴奋:"太棒了!机会难得,马上行动!"
- 😰 焦虑:"怎么办?完了完了,要出大事了!"
- 🤑 贪婪:"不能错过!再不上车就晚了!"
- 😒 嫉妒:"凭什么是他不是我?我也要得到!"
- 😤 抱怨:"都是别人的错,我没有问题!"
- 😔 自卑:"我不行,我做不到,我不配。"
- 😴 拖延:"再等等,现在还不是时候。"
- 🙅 抵制陌生信息:"这不可能!我不信!肯定是假的!"
冷静策略:
- 24小时法则:重大决策等24小时再做
- 第三人称视角:"如果这件事发生在朋友身上,我会怎么建议?"
- 未来视角:"一年后回看,我会后悔这个决定吗?"
- 咨询他人:找一个理性的朋友讨论
观察自己的情绪变化,客观的审视情绪变化的原因。
方法四:关注绝对数字,而非相对数字
核心原则:媒体喜欢用相对数字吓唬你,要学会看绝对数字。
典型套路:
标题:"某药物使心脏病风险增加50%!"
听起来很可怕,但看绝对数字:
- 原本风险:0.002%(万分之二)
- 增加50%后:0.003%(万分之三)
- 实际增加:0.001%
换算:10万人中,从2个人增加到3个人,增加了1个人
对比:
- 不运动的心脏病风险增加:200%
- 吸烟的心脏病风险增加:300%
- 肥胖的心脏病风险增加:150%
结论:这个药物的风险远小于不运动、吸烟、肥胖。
实践方法:
看到相对数字时,问自己:"基数是多少?";"绝对增加了多少?";"和其他风险相比如何?"。
方法五:建立概率思维框架
核心原则:培养用概率思考的习惯。

概率思维的四个层次:
层次1:二元思维(最低级)
- "会发生" vs "不会发生"
- "安全" vs "危险"
- "好" vs "坏"
层次2:概率意识
- "可能发生" vs "不太可能发生"
- "比较安全" vs "比较危险"
- "风险较高" vs "风险较低"
层次3:量化概率
- "发生概率是1%"
- "风险是万分之一"
- "成功率是30%"
层次4:期望值思维(最高级)
- "期望收益 = 概率 × 收益"
- "期望损失 = 概率 × 损失"
- "期望值 = 期望收益 - 期望损失"
实践练习:
场景:决定是否创业
二元思维:"会成功吗?" → 无法回答,陷入焦虑
概率思维:
- 完全成功概率:20%,收益:1000万
- 部分成功概率:30%,收益:100万
- 失败但有收获概率:40%,损失:50万,但获得经验
- 完全失败概率:10%,损失:100万
期望值计算:
- 期望收益 = 20% × 1000万 + 30% × 100万 = 230万
- 期望损失 = 40% × 50万 + 10% × 100万 = 30万
- 期望值 = 230万 - 30万 = 200万
对比:
- 不创业:稳定工资,10年赚200万
- 创业:期望值200万,但有经验和成长
决策:根据个人风险偏好和人生目标决定。
方法六:扩大样本量,避免个案影响
核心原则:不要被个别案例影响,要看统计规律。
典型错误:"我朋友抽烟活到90岁,所以抽烟不一定有害。"这是个案,不是规律。
统计数据:
- 吸烟者平均寿命减少10年
- 肺癌风险增加15-30倍
- 心脏病风险增加2-4倍
- 中风风险增加2-4倍
为什么个案会误导?
- 幸存者偏差:你只看到活到90岁的吸烟者,看不到50岁就去世的
- 样本量太小:一个人不能代表统计规律
- 混淆因素:可能是基因好、饮食好、运动多等其他因素
正确做法:
| 错误 | 正确 |
|---|---|
| "我认识一个人..." | "统计数据显示..." |
| "我听说..." | "研究表明..." |
| "有人..." | "平均来说..." |
实践方法:
听到个案时,问自己:
- "样本量有多大?"
- "有没有大规模研究?"
- "统计数据是什么?"
- "这个个案是例外还是规律?"
记住:个案可以激励,但不能指导决策;决策要看统计,不看故事;一个人的经历不能推广到所有人。
最后的提醒:
理性决策不保证好结果,但长期来看,理性决策的期望值最高。
就像巴菲特说的:"在别人贪婪时恐惧,在别人恐惧时贪婪。"
当所有人都因为飞机失事而不敢坐飞机时,理性的人知道这正是最安全的时候。
当所有人都因为彩票头奖而疯狂购买时,理性的人知道这是最不值得的投资。
不要让恐惧和幻想控制你的决策。
用理性的概率思维,做出更明智的选择。
这,才是真正的自由。
延伸思考
- 回顾你最近的决策:有哪些是被几率谬误或几率忽视影响的?
- 计算你的日常风险:你每天面临的最大风险是什么?和你担心的风险相比如何?
- 检视你的恐惧:你最害怕的事情,实际概率是多少?
- 评估你的投资:你买过彩票吗?买过保险吗?这两个决策一致吗?
- 观察媒体报道:下次看新闻时,注意哪些是小概率事件被放大了?
思考这些问题,你会对自己和世界有更清醒的认识。